
1.设函数f(x)在x=0处连续,且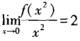 (D)
(D)
A. f(0)=1且f’(0)=2
B. f(0)=0且f’(0)=2
C. f(0)=1且f’+(x)=2
D. f(0)=0且f’+(0)=2
答案解析:
2. (C)
(C)
A.
B.
C.
D.
答案解析: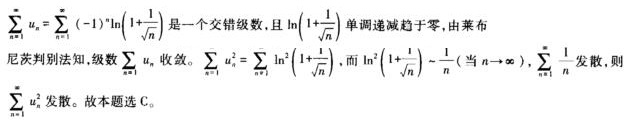
3.下列命题正确的个数是( )。(1)若f(x)是[a,b]上的连续函数,则f(x)在[a,b]上可导;(2)若函数f(x)在[a,b]上可导,则f(x)是[a,b]上的连续函数;(3)“函数f(x)在[a,b]上可导”是“函数f(x)在[a,b]上可微”的充要条件;(4)若f(x)是(a,b)上的连续函数,则f(x)在(a,b)上可积;(5)若函数f(x)在[a,b]上有界,且只有有限个间断点,则f(x)在[a,b]上可积。(B)
A. 2
B. 3
C. 4
D. 5
答案解析:一元函数在闭区间上可导一定连续,但在闭区间上连续不一定可导,所以(1)错误,(2)正确。“函数f(x)在x0处可导”的充要条件是“函数f(x)在x0处可微”,所以(3)正确。一元函数在开区间上连续,不一定可积,例如1/x在(0,1)上连续,其在(0,1)上不可积,所以(4)错误。一元函数在闭区间上连续或在闭区间上有界且只有有限个间断点,则一定可积,但可积不一定连续,所以(5)正确。故本题选B。
4.已知P(A)=1/4,P(B|A)=2/3,P(A|B)=1/2,则P(AB)=( )。(A)
A. 1/6
B. 1/4
C. 1/3
D. 1/8
答案解析:由P(B|A)=2/3,P(A)=1/4,知P(AB)=P(A)P(B|A)=1/6,P(B)=p(AB)/P(A|B)=1/3,所以P(AB)=P(B)-P(AB)=1/6。故本题选A。
5.设A是秩为n-1的n阶矩阵,α1与α2是方程组Ax=0的两个不同的解向量,则Ax=0的通解必定是( )。(D)
A. α1+α2
B. kα1
C. k(α1+α2)
D. k(α1-α2)
答案解析:通解中必有任意常数,A项错误;齐次方程组Ax=0的基础解系中解向量的个数为n-r(A),所以齐次方程组Ax=0的基础解系由一个非零向量构成。由题意无法确定α1是不是零向量,所以kα1可能为零向量,排除B。对于α1+α2,当α1=-α2时,α1+α2=0(即α1≠α2并不能保证α1+α2≠0),排除C;而α1≠α2→α1-α2≠0。故本题选D。
6.已知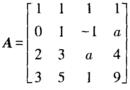 (D)
(D)
A. 3
B. 2
C. 1
D. 1或3
答案解析:
7.《学记》中提出“道而弗牵,强而弗抑,开而弗达”。这体现了下列哪项教学原则?( )(A)
A. 启发式原则
B. 因材施教原则
C. 循序渐进原则
D. 巩固性原则
答案解析:“道而弗牵,强而弗抑,开而弗达”意为教师要引导学生,但决不牵着学生的鼻子;要严格要求学生,但决不使学生感到压抑;要启发学生思考问题,但决不直接把答案告诉学生。教师的作用在于引导、激励、启发,而不是牵着学生走,强迫和代替学生学习。启发式原则(启发性原则)是指在教学中教师要主动承认学生是学习的主体,注意调动他们的学习主动性,引导他们独立思考、积极探索、生动活泼地学习,使学生自觉地掌握科学知识从而提高分析问题、解决问题的能力。因材施教原则是指教师在教学中,既要从课程计划、学科课程标准的统一要求出发,面向全体学生,又要根据学生的个别差异,有的放矢地进行教学,使每个学生都能扬长避短获得最佳的发展。循序渐进原则是指教师要严格按照科学知识的内在逻辑体系和学生认识能力发展的顺序进行教学,使学生系统地掌握基础知识和基本技能,培养学生的逻辑思维能力。巩固性原则是指教师在教学中,使学生在理解的基础上牢固地掌握知识和基本技能,并长久地保持在记忆中,在需要的时候能够准确无误地呈现出来,以利于学生运用知识技能。
8.《普通高中数学课程标准(2017年版)》中指出,命题应依据( ),注重对学生数学学科核心素养的考查,处理好数学学科核心素养与知识技能的关系。(A)
A. 学业质量标准和课程内容
B. 数学内容主线
C. 教材内容
D. 数学文化
答案解析:《普通高中数学课程标准(2017年版)》指出,命题应依据学业质量标准和课程内容,注重对学生数学学科核心素养的考查,处理好数学学科核心素养与知识技能的关系,要充分考虑对教学的积极引导作用。
简答题一项“过关游戏”规则规定:在第n关抛一颗骰子n次,如果这n次抛掷所出现的点数之和大于2n,则算过关。9.这项游戏最多能过几关?
设这项游戏中最多能过n关,骰子出现的点数最大为6,似设每次都能投出6,则有6n≥2n。分析得,6×4>24,6×5<25,当n≥5时,n次出现的点数之和大于2n已不可能,所以n≤4,即这项游戏最多能过4关。解析:10.连过三关的概率是多少?(注:骰子是一个在各面上分别有1,2,3,4,5,6点数的均匀正方体,抛掷骰子落地静止后,向上的点数为出现点数)
连过三关要求第一关时投掷1次的点数大于2,第二次时投掷两次的点数和大于4,第三次时投掷三次的点数和大于8。 第一次过关的概率为4/6=2/3。 第二次过关的基本事件有62种,不能过关的基本事件个数为不等式x+y≤4的正整数解的个数,等价于不定方程x+y=a(a=2,3,4)的正整数解的个数。用隔板法求解,用a=4做一个示范,将4个“1”排成一列,中间有3个空挡,在3个空挡中插入一块隔板(C31),这样就把4个“1”分[***还有5806个字符未阅读,点击下载文档阅读全文***]



