中学教师资格认定考试（初级数学学科知识与教学能力）模拟试卷65

中学教师资格认定考试（初级数学学科知识与教学能力）模拟试卷65单项选择题

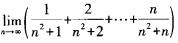1.极限(C)

A. 1

B. 1/3

C. 1/2

D. 不存在

答案解析：因为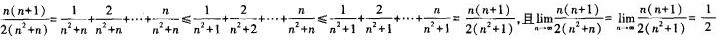，所以由夹逼准则知，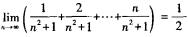

2.已知R³中的一组基为α₁=(1，1，0)^T，α₂=(1，0，1)^T，α₃=(0，1，1)^T，则向量α=(2，0，0)^T在基α₁，α₂，α₃下的坐标是( )。(C)

A. (-1，1，1)^T

B. (1，-1，1)^T

C. (1，1，-1)^T

D. (1，1，1)^T

答案解析：设向量α在基α₁，α₂，α₃下的坐标为(x，y，z)^T，即α=xα₁+yα₂+zα₃，则有解得

3.已知随机变量X的概率密度函数为f(x)=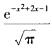(B)

A. 1

B. 1/2

C. 1/3

D. 1/4

答案解析：因为f(x)=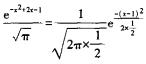

4.在空间右手直角坐标系中，向量α，β，γ的坐标依次为(1，0，-1)，(1，-2，0)，(-1，2，1)，则(3α+β-γ)×(α-β+γ)的坐标为( )。(A)

A. (16，4，16)

B. (16，-4，16)

C. (-16，4，16)

D. (16，4，-16)

答案解析：3α+β-γ的坐标为(5，-4，-4)，α-β+γ的坐标为(-1，4，0)，所以(3α+β-γ)×(α-β+γ)=

5.下列数列收敛的是( )。

B解析：A项中，当n→∞时，{(-1)ⁿ}的极限不存在，该数列发散；B项中，因为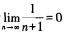，所以数列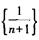收敛；C项和D项中，因为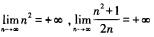，所以数列{n²}和数列

6.设A为n阶方阵，r(A)=3＜n，则在A的n个行向量中( )。(B)

A. 任意3个行向量都是极大线性无关组

B. 至少有3个非零行向量

C. 必有4个行向量线性无关

D. 每个行向量可由其余n-1个行向量线性表出

答案解析：任意3个线性无关的行向量都是行向量组的极大线性无关组，A项错误；极大线性无关组中不能有零向量，因为r(A)=3，所以至少有3个非零向量，B项正确；若有4个行向量线性无关则r(A)≥4，与题设矛盾。C项错误；对角矩阵

7.在某教师设计的“反比例函数的图像和性质”的教学目标中，“通过反比例函数图像画法的全过程，体会无限趋近的思想”属于以下哪一方面的内容?( )(B)

A. 知识技能

B. 数学思考

C. 问题解决

D. 情感态度

答案解析：《义务教育数学课程标准(2011 年版)》指出，“经历借助图形思考问题的过程，初步建立几何直观”“能独立思考，体会数学的基本思想和思维方式”都属于数学思考的课程目标。所以“通过反比例函数图像画法的全过程，体会无限趋近的思想”属于数学思考方面的内容。

8.《义务教育数学课程标准(2011 年版)》在“推理能力”中提到，“推理”一般包括( )。(C)

A. 逻辑推理和类比推理

B. 逻辑推理和演绎推理

C. 合情推理和演绎推理

D. 类比推理和合情推理

答案解析：推理是数学的基本思维方式，也是人们学习和生活中经常使用的思维方式。推理一般包括合情推理和演绎推理。

简答题某市旅游局为了了解游客情况，针对情况制定策略，在某月中随机抽取甲、乙两个景点各10天的游客数，统计得到茎叶图如下：

9.若将图中景点甲中的数据作为该景点较长一段时期内的样本数据，以每天游客人数频率为概率P。今从这段时期内任取4天，记其中游客数超过130人的天数为ξ，求P(ξ≤2)；

根据茎叶图知，景点甲中游客数超过130人的概率为4/10=2/5。根据题意知，随机变量ξ～B(4，2/5)，所以P(ξ≤2)=P(ξ=0)+P(ξ=1)+P(ξ=2)=C₄⁰(2/5)⁰(3/5)⁴+C₄¹(2/5)¹(3/5)³+C₄²(2/5)²(3/5)²=513/625。解析：

10.现从上图20天的数据中任取2天(甲、乙各1天)，记其中游客数不低于125且不高于135人的天数为η，求η的分布列和数学期望。

根据茎叶图知，景点甲中游客数不低于125人且不高于135人的概率为1/10；景点乙中游客数不低于125人且不高于135人的概率为2/5。 根据题意知，η的取值为0，1，2。 [*] η的分布列如下表： [*]解析：

11.求由曲线y=3-x²和y=1-x所围的平面图形的面积S。

联立方程可求得两曲线的交点坐标为(-1，2)和(2，-1)，因此由定积分的几何应用可知S=∫_-1²[(3-x²)-(1-x)]dx=∫_-1²(2+x-x²)dx=[*] [*]解析：

12.已知矩阵

两矩阵相似，则tr(A)=tr(B)(矩阵的迹：主对角线元索之和)，｜A｜=｜B｜。因为A～B，所以有[*]解得a=7，b=-2。B=[*] ｜λE-A｜=[*]=(λ-5)(λ+1)=0，解得λ=-1或5。 当λ=-1时，(-E-A)=[*]，特征值-1对应的特征性向量为α₁=(-2，1)^T； 当λ=5时，(5E-A)=[*]，特征值5对应的特征性向量为α₂=(1，1)^T。 令P₁=(α₁，α₂)=[*]，则P₁^-1AP₁=Λ=[*]。 因为两矩阵相似，所以矩阵B的特征值也为-1和5。进而有， 当λ=-1时，(-E-B)=[*]，特征值-1对应的特征性向量为β₁=(-1，1)^T； 当λ=5时，(5E-B)=[*]，特征值5对应的特征性向量为β₂=(-7，1)^{[***还有4143个字符未阅读，点击下载文档阅读全文***]}